(Versión imprimible, ir a la versión completa)
| Índice | Introducción | Capítulo 1 | Capítulo 2 | Capítulo 3 | Capítulo 4 | Capítulo 5 |
CAPÍTULO 5. Orientándose en el Universo |
||

Van Gogh, Noche estrellada |
||
1. Los movimientos de la Tierra |
||
|
Antes de centrarnos en los movimientos y las coordenadas celestes, es importante tener claro lo que ocurre aquí, en la Tierra. La Tierra tiene tres movimientos fundamentales:
|
||
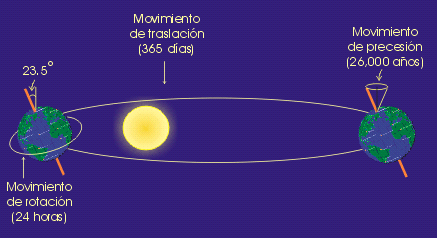
Fig.5.1. Movimientos de la Tierra |
||
 |
||
1.1 Tiempo sidéreo |
||
|
La combinación de los movimientos de rotación y traslación produce una aparente paradoja: la medida del día es distinta si se mira respecto al Sol o respecto a las otras estrellas, que al estar muchísimo más lejos, pueden ser consideradas como fijas. El período de rotación de la Tierra, como hemos visto, es de 23 horas, 56 minutos, 3.5 segundos. Éste es el tiempo que tarda un determinado punto de la Tierra en volver a su posición respecto a las estrellas fijas, y es a lo que se llama día sidéreo. Sin embargo, para que ese punto determinado vuelva a estar en la misma posición respecto al Sol, tiene que girar, además de los 360 grados necesarios para completar su rotación, un ángulo extra igual a 360/365 grados, ya que éste es el ángulo que recorre la Tierra en un día en su traslación alrededor del Sol. En realizar este giro, tarda los 3 minutos, 56.5 segundos que hacen que el día solar tenga 24 horas. Este hecho es el que provoca que veamos aparecer las estrellas en el horizonte cada día aproximadamente 4 minutos antes. |
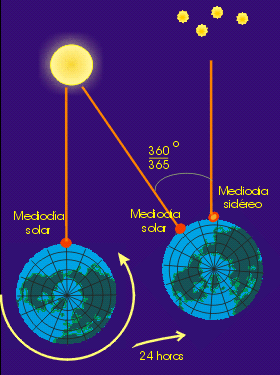
Fig.5.2. Día sidéreo |
|
 |
||
2. Coordenadas terrestres |
||
|
Antes de intentar orientarnos en el cielo, es bueno tener claras cuáles son las referencias en la Tierra. Al fin y al cabo, la orientación celeste es bastante similar a la terrestre, ya que en los dos casos tenemos que establecer unas coordenadas sobre una superficie esférica. La base de las coordenadas celestes, como veremos, es suponer que el cielo es una esfera que rodea a la Tierra. Las líneas imaginarias que nos ayudan a orientarnos en la Tierra son los paralelos y los meridianos. Los paralelos son círculos contenidos en planos perpendiculares al eje de la Tierra, y como su nombre indica, son paralelos unos a otros. El ecuador es un paralelo que divide a la Tierra en dos Hemisferios iguales, y es el único paralelo que es también un círculo máximo. |
||
|
Los meridianos son círculos máximos perpendiculares al ecuador, que pasan siempre por los dos polos de la Tierra. El Ecuador es la referencia para medir la latitud. Decimos que un punto está a una latitud de 20 grados Norte cuando ese punto está situado a 20 grados al Norte del Ecuador. La longitud no tiene un punto de referencia "natural", ya que todos los meridianos son absolutamente iguales unos a otros. Sin embargo, para poder orientarnos y decir que un punto está al Este o al Oeste, hay que indicar respecto a qué meridiano. Por razones históricas, el meridiano elegido como meridiano cero, a partir del cual se comienza a contar hacia el Este o al Oeste, es el meridiano que pasa por el observatorio de Greenwich (Inglaterra). |
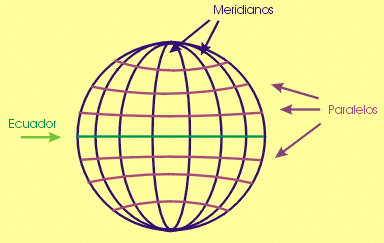
Fig.5.3. Paralelos y meridianos en la Tierra |
|
|
Sin embargo, el meridiano de Greenwich tardó en ser adoptado mundialmente. En 1871, en el primer congreso geográfico internacional se pusieron de acuerdo en utilizar el mismo punto de referencia en todos los países, eligiéndose como referencia el meridiano de Greenwich. Hasta ese momento, existían varios meridianos que eran adoptados por cada país. En España, por ejemplo, se utilizaba el meridiano del observatorio de San Fernando, en Cádiz. A partir de esta conferencia, aunque en los mapas locales y las cartas marinas se utilizaban los meridianos elegidos por cada país, se empezaron ya a dar las posiciones de los barcos referidas al meridiano de Greenwich. |
||
 |
||
3. Coordenadas celestes |
||
|
Si alguien nos dice "mira esa estrella en el cielo", le pediremos que nos indique de alguna manera dónde está esa estrella. Es difícil orientarse en un sitio donde no hay aparentemente referencias. Quizá nos pueda decir que la estrella está a una cierta altura sobre el horizonte, y a una cierta distancia a la derecha de un árbol. Pero es evidente que para determinar realmente la posición de un objeto en el firmamento, necesitaremos definir unas coordenadas, de la misma manera que se hace en la Tierra. |
||
3.1 Coordenadas altacimutales |
||
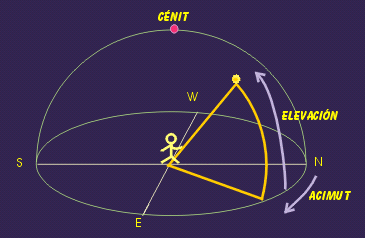
Fig.5.4. Sistema de coordenadas altacimutal |
Las coordenadas altacimutales siguen las indicaciones que alguien nos daría al señalar una estrella. La altura o elevación es el ángulo que forma la posición del objeto con el horizonte. Y el acimut es el ángulo que forma la posición del objeto con un punto de referencia, que por convenio es el Norte. De esta forma, en el Este el acimut será 90 grados, en el Sur 180 y en el Oeste 270 grados. El problema que tienen estas coordenadas es que no son fijas para cada objeto en el cielo, sino que varían dependiendo de la posición del observador. Por ejemplo, un observador en el Polo Norte, tendría la estrella polar justo encima de su cabeza, en el punto denominado cénit, por tanto, para este observador, la estrella polar estaría a una elevación de 90 grados. Sin embargo, un observador que estuviese en el ecuador, apenas alcanzaría a ver la estrella polar, ya que ésta se encontraría en el horizonte, es decir, a una elevación de 0 grados. |
|
|
Otro problema que tiene este sistema de coordenadas, es que la estrellas van variando su posición en el cielo a lo largo de la noche. Como sabemos, debido al movimiento de rotación de la Tierra, las estrellas aparecen en el cielo por el este y parecen describir un círculo alrededor de la estrella polar, hasta que se ponen por el oeste. Esto supone que a lo largo de la noche, el acimut y la elevación de una estrella va cambiando, pasando por un punto de elevación máxima que es donde se dice que el objeto culmina. Vemos por tanto, que este sistema de coordenadas no es verdaderamente útil para definir la posición de un objeto en el firmamento, pero sí que puede serlo, por ejemplo, para indicar la posición de un radiotelescopio con montura altacimutal, ya que da una idea muy clara de hacia donde se está observando. |
||
 |
||
3.2 Coordenadas ecuatoriales |
||
|
Para poder determinar la posición de las estrellas de una manera clara y con unas coordenadas fijas independientemente del lugar de observación, los astrónomos inventaron un sistema de coordenadas denominado sistema de coordenadas ecuatorial. Para tener una idea clara de qué significan estas coordenadas, vamos a imaginarnos que la Tierra está en el centro del universo, rodeada por una esfera que contiene al Sol y todas las estrellas. |
||
|
Si prolongamos el plano del ecuador terrestre, tendremos un plano que divide en dos hemisferios a la esfera celeste, que, al igual que en la Tierra, se denominan Hemisferio Norte y Hemisferio Sur. De la misma forma, la prolongación del eje de la Tierra, cortará a la esfera celeste en los Polos Norte y Sur celestes. Si trazamos círculos paralelos al ecuador celeste, y otros círculos perpendiculares a él que pasen por los polos celestes, tendremos un sistema de referencia en el cielo muy similar al de paralelos y meridianos que utilizamos en la Tierra. Podremos, entonces, dar la posición de una estrella, diciendo los grados que ésta se separa hacia arriba o hacia abajo del ecuador celeste, a lo que denominaremos declinación y cuánto se desvía hacia el este u oeste de un punto determinado (ascensión recta). En este punto volvemos a tener el mismo problema que con el meridiano cero de las coordenadas terrestres. Hace falta establecer un meridiano como punto de partida de las medidas de ascensión recta, y se ha elegido el denominado equinoccio vernal o punto de Aries. Este punto es aquél en el que se encuentra el Sol en el equinoccio de primavera, uno de los dos puntos en los que se cruzan la eclíptica y el ecuador celeste. |
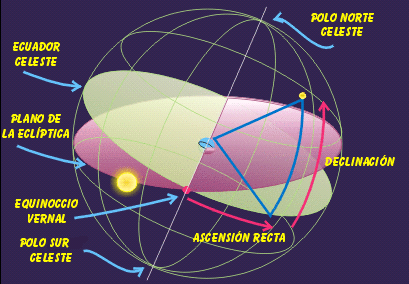
Fig.5.5. Sistema de coordenadas ecuatorial |
|
|
La eclíptica es la trayectoria aparente que describe el Sol respecto a las estrellas fijas a lo largo del año. Como sabemos, son la Tierra y el resto de los planetas los que giran alrededor del Sol, y todos lo hacen aproximadamente en el mismo plano, denominado plano de la eclíptica. Esto quiere decir que, desde la Tierra siempre veremos al Sol y al resto de los planetas moviéndose respecto a las estrellas fijas en la zona del cielo donde se encuentra la eclíptica. Finalmente es interesante introducir el concepto de ángulo horario, que no es más que la diferencia entre la ascensión recta de la fuente a observar y nuestra hora siderea. Dicho ángulo se mide en grados. Si el ángulo horario es positivo, significa que la fuente no ha llegado todavía al meridiano en que nos encontramos y se encuentra hacia el Este. Si es negativo, la fuente ya ha rebasado el meridiano y se encuentra hacia el Oeste. Un ejemplo de cómo calcular el ángulo horario sería el siguiente: Sea una fuente con ascensión recta igual a 17 h 00 m 00 s (es decir, se encuentra a 17*15=255º al Este del punto vernal). Supongamos que nuestro reloj sidereo marca las 10h 00m 00s (es decir, estamos también nosotros a 10*15=150º al Este del punto vernal). En este caso, a la fuente le faltan 17-10=7 horas para llegar al meridiano donde nos encontramos. Una vez definidas las dos referencias (ecuador y equinoccio vernal), ya tenemos el sistema de coordenadas ecuatorial. Así, llamamos declinación al ángulo, medido en grados, que forma la fuente con el plano ecuatorial celeste (grados positivos cuando la estrella está en el Hemisferio Norte y negativos cuando está en el Hemisferio Sur); y ascensión recta al ángulo, medido en horas, minutos y segundos entre la estrella y el meridiano cero celeste (punto de Aries). Por lo tanto, la declinación varía entre -90 y 90 grados, mientras que la ascensión recta lo hace entre 0 y 24 horas. Este sistema de coordenadas, que aparentemente debería ser inmutable, ya que no depende del punto de la Tierra desde el que se observa, en realidad tiene un pequeño inconveniente. Cuando se estableció, los astrónomos no eran conscientes del movimiento de precesión de la Tierra, (ni de otros movimientos en los que no vamos a entrar), pero estos movimientos provocan que las coordenadas de las estrellas varíen ligeramente con los años. Este cambio es evidente si consideramos, por ejemplo, que Vega estaba situada en el polo norte celeste (donde ahora está Polaris, nuestra estrella polar) hace algo más de 14,000 años y que lo volverá a estar dentro de otros 12,000 años. Debido a estos movimientos, los astrónomos tienen que actualizar sus catálogos con las nuevas coordenadas de los objetos, y siempre indicar junto a las coordenadas el año al que están referidas. |
||
 |
||
3.3 Coordenadas galácticas |
||
|
Las coordenadas galácticas también se utilizan en Astronomía, y tienen como referencia el centro y el plano de nuestra galaxia. Son útiles para saber, sobre todo, la posición de un objeto en el plano galáctico. La latitud galáctica (b) es la distancia en grados que se separa un objeto hacia el norte o sur del plano galáctico, y la longitud galáctica (l) es la distancia en grados que se separa un objeto del centro galáctico. Vemos, por tanto, que el plano galáctico hace las veces de ecuador en estas coordenadas, mientras que el centro galáctico sirve de referencia al igual que lo hacía el equinoccio vernal o el meridiano de Greenwich en las coordenadas ecuatoriales celestes o geográficas, respectivamente. En la siguiente figura se muestra la imagen de nuestra galaxia en rayos gamma representada en coordenadas galácticas. El punto rojo señala el centro galáctico , que, visto desde la Tierra, está en la constelación de Sagitario. El plano galáctico está localizado en b=0, y en la figura se aprecia que es la zona con más emisión. |
||
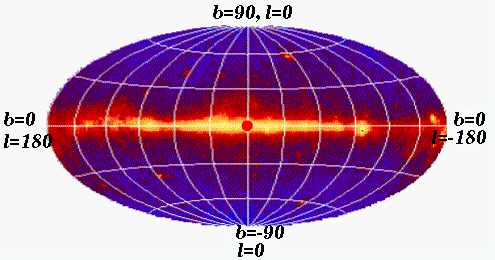
Fig.5.6. Vista de nuestra galaxia en coordenadas galácticas. Satélite Egret. Cortesía de NASA. |
||
 |
||